“总是拿不准,我最纠结了!”
无论是年轻人去相亲,做职业选择,还是创业方向谋划,都离不开贝叶斯定律难题。
事实上,我们的祖先在很早以前,就通过开发游戏帮助我们训练一种好思维,别以为那些古老游戏是浪费时间。
那么,我们玩那一款游戏最容易炼成一种好的心智呢?
换一个话题,就是:“最符合贝叶斯定律的中国传统游戏是哪一款?”
要回答这个问题,我们需要先明确贝叶斯定律(Bayes'Theorem)的核心逻辑:
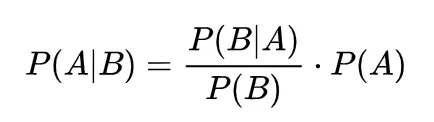
简单说吧,贝叶斯定律的精髓在于:在不完全信息的情况下,通过不断收集新的证据(B),来动态调整对原有假设(A)发生概率的判断。
基于这个核心逻辑,中国传统游戏中最符合贝叶斯定律的,非“藏钩”(这里读“Canggou”)莫属。

“藏钩”是中国古代非常流行的一种游戏,尤其在汉代至唐宋时期。玩法通常是:一群人分为“藏”方和“猜”方。藏方将一枚小钩子(或类似的小物件)藏在某个人的一只手中,然后大家把手背在身后互相传递、混淆视听。最后,大家把手伸到身前握拳,让猜方的人来猜钩子在谁的手里。

为什么它符合贝叶斯定律?
藏钩游戏,完美模拟了贝叶斯推理的全过程:
先验概率(P(A)):
在游戏开始前,或者第一轮猜测时,猜方对于钩子在谁手里没有任何信息。因此,他会假设一个先验概率。例如,如果有10个人藏钩,他会认为每个人手里有钩子的概率都是10%。
似然概率(P(B|A)):
随着游戏进行,藏方的人会有动作、表情或言语的暗示(无论是真实的还是伪装的)。
假设A是“张三手里有钩子”。
假设B是“张三的手在传递时停顿了一下”。
猜方需要判断:如果张三手里真的有钩子,他做出“停顿”这个动作的概率是多少?(这是似然概率)。
后验概率(P(A|B)):
当猜方观察到“停顿”这个新证据(B)后,他会运用贝叶斯公式更新他的判断。他会提高对张三的怀疑度,降低对其他人的怀疑度。
动态迭代:藏钩往往不是一次定胜负,而是多轮传递。每一次传递、每一次眼神交流,都是新的证据。猜方需要不断地根据新信息推翻旧的判断,重新计算概率分布。
藏钩是一个纯粹的“不完全信息动态博弈”。猜方的大脑就是一个贝叶斯计算器,通过观察对手的微表情和动作(数据),不断修正自己的信念(概率分布)。
当然,我国古老游戏中,还有几款是符合贝叶斯逻辑的游戏。比如,射覆,可能是更高级的抽象贝叶斯。玩法是,把一个物品藏在碗或盆下面,让人猜里面是什么。这款游戏比藏钩更难,猜者不仅要观察藏者的神态,往往还需要结合当时的环境、时间、甚至通过占卜(如易经)来获取“证据”。
猜枚又是一款好玩的游戏,类似于现在的“石头剪刀布”或“猜豆子”。一人手握若干枚棋子或豆子,让对方猜单双数或具体数量。虽然规则简单,但高手过招时,会根据对手上一把出的是单数还是双数,来推断他下一把的心理策略。如果对手连续三次出单数,猜者会根据“均值回归”或“惯性”的假设,更新下一把是双数的概率。
此外,我们几乎人人都会玩的麻将,被专家们认为是最复杂的贝叶斯网络。
以四人麻将游戏为例,它要经过听牌判断:你需要根据桌面上打出的牌(证据B),来推断对手是否听牌(假设A);还要做绝张判断:你需要根据牌墙剩余的牌数和已经出现的牌,计算某张牌还存在的概率。
麻将高手之所以心智强大,是因为他们能根据对手的出牌顺序和吃碰杠的行为,实时更新对各家手牌结构的概率模型。
贝叶斯定律的本质是“通过新证据修正旧信念”的游戏。如果拿麻将与藏钩比较,藏钩是理论上的最佳答案,其规则就是“观察-推理-更新-再观察”的循环,且信息的获取是渐进式的,非常纯粹。而麻将则是实战中最复杂的答案。它包含了海量的变量和多人博弈的心理战,是对贝叶斯网络最复杂的应用。
所以,如果你想体验古人是如何进行“贝叶斯推理”的,藏钩是最原汁原味的选择。
这就不难理解,平时我们见到自己身边玩牌玩的最好的,往往在各个方面都比较厉害。
写到这里,我突然有个感悟:中华文明之所以永续不绝,这可能与我们的祖先们喜欢玩的古老游戏有关吧。